Frequency Modulation ( FM )

Theory

The formula for an FM signal, s ( t ), is given by

Where,
m ( t ) = modulating signal
f c = carrier frequency
A c = carrier amplitude

If we let the modulating signal be a pure sinusoid, m ( t ) = Am   cos 2 π f m t , then equation ( 1 ) becomes,


There are two types of FM depending on the value of β.

The Block level implementation of the Frequency Modulation Process can be seen in the Fig.1 below.

Fig.1 Block level design of FM wave.

FM applications are divided into two broad categories:
  • Wideband FM ( WFM )
  • Narrowband FM ( NBFM )

The primary difference between the two types of FM is the number of sidebands in the modulated signal. Wideband FM has a large number ( theoretically infinite ) number of sidebands. Narrowband FM has only a single pair of significant sidebands. It is possible to determine if a particular FM signal will be wide or narrow band by looking at a quantity called the Deviation Ratio (DR). It is defined as the ratio of the maximum deviation of the FM signal to the maximum modulating frequency:
D R = δ / f max

NBFM ( β < < 1 )
If β is much less then 1, we have Narrow Band Frequency Modulation ( NBFM ). Equation (2) can be approximated as

WBFM ( All β )
The Wide Band Frequency Modulation formula is valid for all β. The approximations used for NBFM are not accurate here. Using Fourier series coefficients, Equation (2) for WBFM can be written as


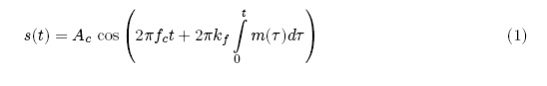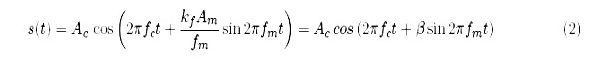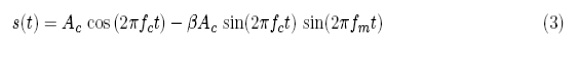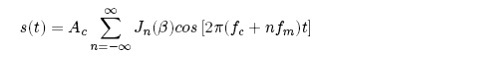An important concept in the understanding of FM is that of Frequency Deviation. The amount of frequency deviation a signal experiences is a measure of the change in transmitter output frequency from the rest frequency of the transmitter. The rest frequency of a transmitter is defined as the output frequency with no modulating signal applied. For a transmitter with linear modulation characteristics, the frequency deviation of the carrier is directly proportional to the amplitude of the applied modulating signal. Thus an FM transmitter is said to have a modulation sensitivity, represented by a constant , k f , of so many kHz / V, k f = frequency deviation / V = k f kHz / V.


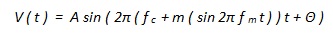FM Analysis
From the definition of frequency deviation, an equation can be written for the signal frequency of an FM wave as a function of time: