Amplitude Modulation

Theory


Amplitude Modulation

In amplitude modulation, the amplitude of the carrier is varied according to variations in the amplitude of the modulating signal. The frequency of the carrier remains same while its amplitude varies according to amplitude variation of the modulating signal.

Let us represent the modulating signal by em

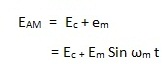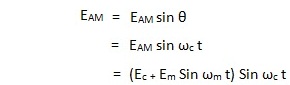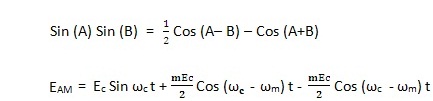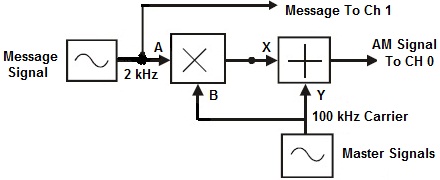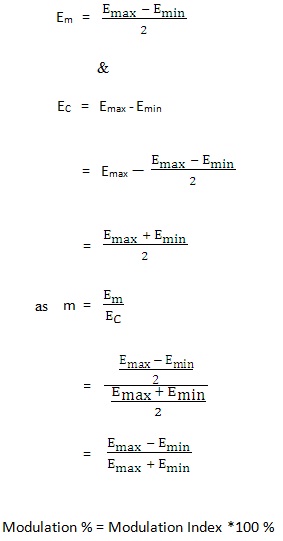em = Em Sin ωm t
And carrier signal can be represent by ec
ec = Ec Sin ωc t

Where Ec is maximum amplitude of modulating signal, Ec is maximum amplitude of carrier signal, ωc is frequency of modulating signal and ωc is frequency of carrier signal.




We know that


Need for modulation
  1. To send a signal over long distance it requires more energy. Energy and frequency are related by the Planck’s Formula.

    E = hv
    where
    • E is Energy of the signal,
    • h is Planck’s constant,
    • and v is Frequency of signal.
    So when the frequency is low, energy will be low, to increase the energy of the signal we need to increase the frequency, this is achieved by modulation.

  2. For transmitting a signal of wavelength λ the antenna length must be λ/4. So if we want to send a 1Hz ( λ = 3*108 m ) signal using an antenna, its length must be 75,000 Km, and it is impossible. So to reduce the length of antenna the frequency of information signal is increased by modulation using a much higher frequency carrier.


    Fig.1 Block diagram of setup of this AM Modulation experiment.


    Modulation Index and Percentage Modulation
    The ratio of maximum amplitude of modulating signal to maximum amplitude of carrier signal is called modulation index.


    Value of Em must be less than the value of Ec to avoid any distortion in the modulated signal. Hence maximum value of modulation index will be equal to 1, when Em = Ec. Minimum value will be zero. If modulation index is higher than 1, then it is called over modulation. Data is lost in such case. When modulation index is represented in percentage it is called percentage modulation.

    Calculation of modulation Index: - This is called time domain representation of AM signal.