Binary Phase Shift Keying ( BPSK ) Demodulation

Objective

To study the Demodulation of BPSK ( Binary Phase Shift Keying ) signal using product detector.

Introduction

Demodulating a BPSK signal using a product detector is really just DSB - SC signal with a digital message instead of speech or music, it can be recovered using any of the DSBSC demodulation schemes.

If the input waveform is a carrier:

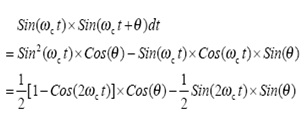X(t) = Sin ( w_c t )
The delayed signal will be:
Y(t) = Sin (w_c t + θ )
where θ is the phase shift of the delayed waveform with respect to the present waveform. The output from the multiplier will then be: For a typical BPSK system, there are many carrier cycles per data period. For ideal operation θ is 0° or 180° and then the second term can be ignored, leaving a DC component plus a large ripple.

A binary phase-shift keying (BPSK) signal can be defined by s ( t ) = A m ( t ) cos 2π f_c t,                                          0 < t < T
Where A is a constant, m ( t ) = + 1 or - 1, f_c is the carrier frequency, and T is the bit duration. The signal has a power P = A² / 2, so that A = √ 2P. Thus the above equation can be written as

where E = PT is the energy contained in a bit duration & if   Φ₁ ( t ) = √ 2 / T cos 2π f_c t  as the orthonormal basis function, shown in the Fig.1 below.


Fig.1 BPSK Constellation diagram.